DATA MATRIX BARCODE

Format of the DATA MATRIX

Length	Type	Checksum
from 1 to 3116 digits (variable)	numeric, alphanumeric or byte	yes (Reed-Solomon)

The encoded data size depends on the type and the length od the data to data to code.

An intermediate structure of 8 bits is used to save each data: the codeword.

A symbol is composed of 3 groups of codewords:

Data codewords: encoded from the data
Stuffing codewords: not mandatory, fill the symbol when data codeword does not complete it
Correction codewords: Based on data and stuffing codewords, it's a Reed-Solomon checksum which allows to retrieve each part of the data in case of reading error.

The encoding requires 2 steps:

High level encoding: consists in the conversion in codewords of the data, adding some stuffing codewords and calculating the checksum one
Low level encoding: consists to position these codewords in the data matrix.

Graphic representation of the DATA MATRIX

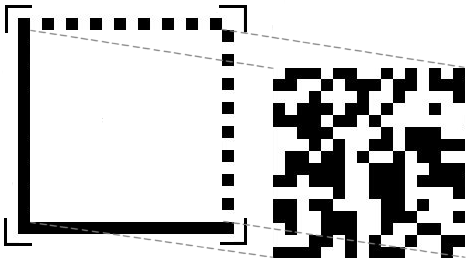
A symbol is composed of black and white rectangular patterns called "cells" or "modules".

A module represent a bit: usually black for the "1" and white for the "0".

The DATA MATRIX can be a square (mostly used) or rectangular.

The symbole can be decomposed into 3 parts:

The "finder pattern", which forms the shape of the data. There are two adjacent segments representing L, consisting of black modules only to determine the direction and orientation data. The two opposite sides alternate black and white modules to determine the size of a module, and therefore the symbol, but also to delimit the symbol
The "quiet zone", which is a white area of at least one module located around the locating units, so that the decoder is not impaired when reading
The data matrix which is composed of modules in the form of a matrix and which is in the center of the tracking units.

When the symbol exceeds a certain size limit, the symbol is divided into data areas, regions, which are defined by internal locating designs. Four types of division into regions exist: 3 for square and 1 rectangular shape.

High level encoding

Six encoding modes coexist: ASCII, Text, C40, X12, EDIFACT and Base 256. The ASCII encoding is the default encoding and the most used. It will be presented here only.

The set of values of the ASCII mode codewords are visible in the following table:

Codeword value	Meaning
1 - 128	ASCII characters (ASCII value + 1)
129	first stuffing character
130 - 229	Number between 00 and 99 (numeric value + 130)
230	Begin C40 encoding
231	Begin Base 256 encoding
232	FNC1
233	Structured append. Allows a message to be split across multiple symbols
234	Reader programming
235	Upper Shift - Set high bit of the following character
236 - 237	05 Macro - 06 Macro
238	Begin ANSI X12 encoding
239	Begin Text encoding
240	Begin EDIFACT encoding
241	ECI - Extended Channel Interpretation code
242 - 255	Not used

Some of the values will not be explained because not used in the ASCII explanation.

In the ASCII mode, some data are encoded according to three possibilities:

The value of a non-extended ASCII codeword (from 0 to 127) equals "ASCII value + 1"
The value of a non-extended ASCII codeword (from 128 to 255) is encoded with 2 codewords: the first, called Upper Shift, equals "235" and the second equals "ASCII value - 127"
Numbers are encoding in a single codeword by group of 2 figures which is equals to "Numeric value + 130".

When the number of data codewords can completely fill the "data" part of the symbol smaller possible codewords filler are added. The first of these codewords, which indicates the end of data in this case is always "129". Following is calculated using the following algorithm 253-state:

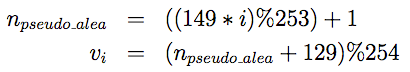
with "%" the modulo and v_i the stuffing codeword at position i

Calculation of correction codewords

The Reed-Solomon codes are used as error correction system. They have a capacity of detection and correction of errors defined in advance, depending on the size of the data matrix.

A body C is a set of elements provided with two closed and called binary operations addition and multiplication. Being closed means that the result of each operation on two elements of the assembly will always be an element of the assembly.

There are many bodies, finite and infinite. It turns out that for any integer prime p and any integer n (>=1), there exists a unique finite n^p elements, noted GF(n_p). These bodies are called Galois fields.

We can represent the elements of GF(n_p) using the basic elements of a : 0, 1, a, a², a³, ..., a^(n-1). Let's take an example:

a³ + a + 1

Elements can also be represented in different forms: binary, decimal, or even in the form of a polynomial. For the same example as:

binary: 1011 (0 indicates no a²)
decimal: 11 (8+2+1)
polynomial: a³ x³ + a x + 1

For each Galois field, there is at least one primitive polynomial, denoted by p (x), which allows to build the body. Data Matrix storing data of 8 bits (in codewords), and therefore work in the Galois field GF(2⁸). They use the primitive polynomial x⁸+x⁵+x³+x²+1, which corresponds to the value 301.

The addition and subtraction of two elements is the XOR (exclusive OR) between these two elements. Multiplication and division are calculated by multiplying the corresponding polynomials. This operation is relatively expensive in computation time, an algorithm is used. Since all components are a power of primitive polynomial p, must be sought for each element c, i power as:

i = log_p (c)
c = antilog_p (i)

From there, we can calculate for two elements c and d:

c * d = antilog_p (log_p(c) + log_p(d))
c / d = antilog_p (log_p(c) - log_p(d))

We can get the e antilogs table thanks to this algorithm:

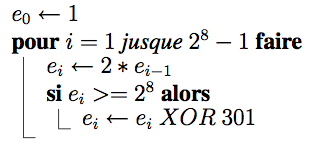
A Reed-Solomon code of length n with k data is noted RS(n,k). So there is n-k = 2t check symbols and this code can correct up to t erroneous symbols. The number of control symbols is defined by the size of the Data Matrix.

The equation for encoding a RS(n,k) code is:

c(x) = i(x) x^n-k + [i(x) x^n-k] modulo g(x)

with

c(x) : the final polynomial
i(x) : the data polynomial
[i(x) x^n-k] modulo g(x) : the control polynomial
g(x) : the generator polynomial

The 2t check symbols are derived from a polynomial power generator 2t, 2t + 1 compound words, which is of the following form:

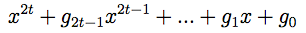
There are 16 block lengths of Reed-Solomon possible (see summary table). The coefficients of the generator polynomials can be calculated using the following algorithm:

Once the generator polynomial calculated, we simply follow the equation to obtain the control polynomial: it is the rest of the division between the data polynomial and the generator polynomial. Coefficients correspond to codewords control.

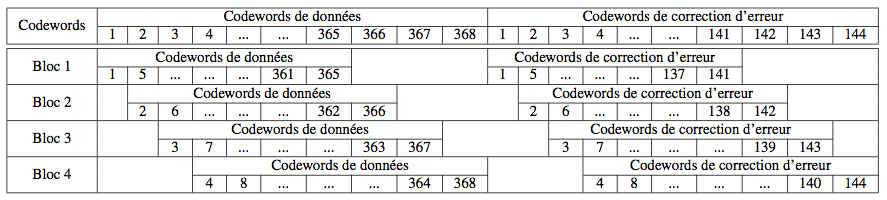
For Data Matrix symbols containing a total of less than 255 codewords (all symbols rectangular and square sizes less than 48x48), the codewords correction are calculated directly from the data codewords. For other symbols, the codewords correction are calculated in accordance with a procedure of interleaving: dividing the codewords into several data blocks of same size and correction codewords are computed block by block. Each codeword c is part of the group:

c modulo n

with n the number of blocks for the symbol

For simplicity, for n blocks, the first group consists of data codewords 1, n +1, 2n +1, 3n +1, ... the second group of data codewords 2, n +2, 2n +2, 3n +2,...

An example of interleaving can be viewed as follows:

Low level encoding

Each codeword is represented in the data matrix by a square part of 8 modules, corresponding to 8 bits. Module 1 has the value of the most significant bit (value 128), while the module 8 has the value of the most insignificant bit (value 1).

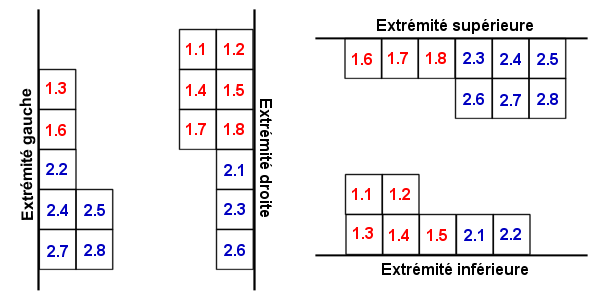
It is however possible that a codeword can not be contained entirely within the matrix at a certain location. These can then be separated into parts (2 or 3) to be continued on the other side of the symbol.

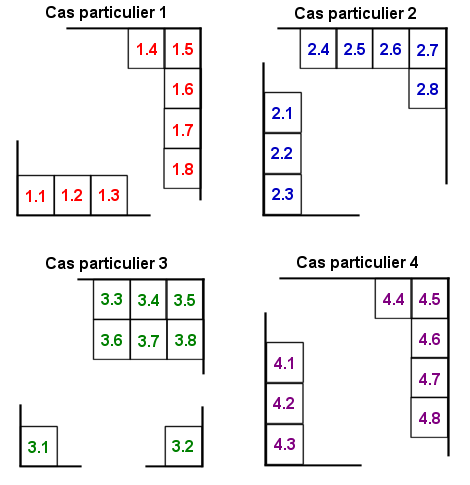
In addition, in four cases, the codewords placed in the corners can also be placed differently.

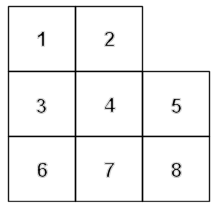
Placement in the matrix follows a certain order. The initial codewords are always placed as follows:

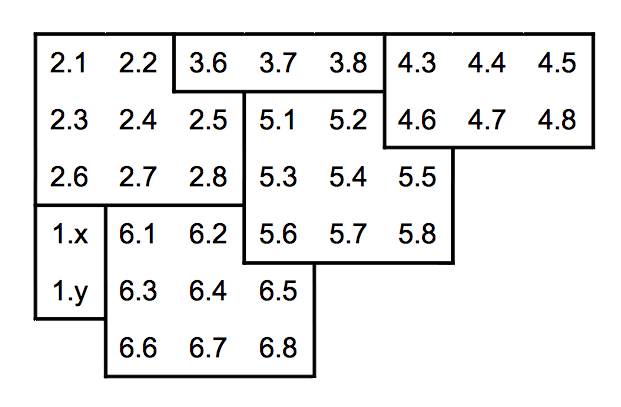
The codewords are then nested in the other, following the oblique lines (45 °) in parallel. The meaning is identical slashes half the time.

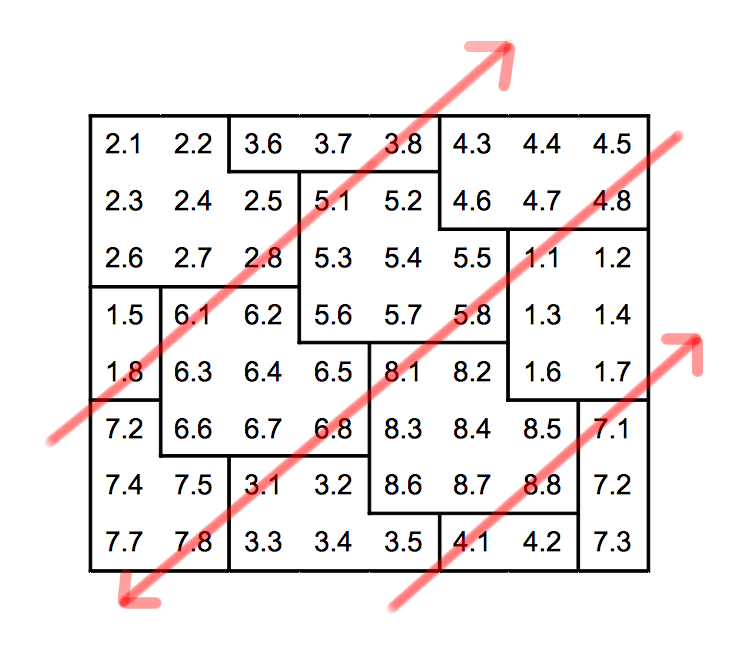
It may, depending on the size of the symbol, the four modules of the lower right corner are empty. Symbols 12x12 example, the data matrix is 10x10, which give 100 modules in 12 codewords can be inserted. Knowing that a codeword full 8 modules, a total of 96 modules will be occupied and the last 4 remain empty. To fill, use of alternating black and white modules as shown below:

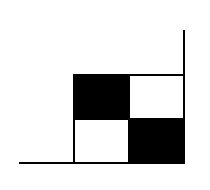
It will then add the finder pattern and possibly the main internal finder pattern if the number of regions is greater than 1.

Encoding example

Suppose we want to encode "ENC01." ASCII values of the characters are:

E	N	C	0	1
69	78	67	48	49

Depending on how ASCII, the values of codewords will be:

Codeword	Method	Evaluation	ASCII value	Binary value
C1	ASCII value + 1	69 + 1	70	0100 0110
C2	ASCII value + 1	78 + 1	79	0100 1111
C3	ASCII value + 1	67 + 1	68	0100 0100
C4	Numeric value + 130	1 + 130	131	1000 0011

The value of codewords 1, 2 and 3 were calculated simply by using the "ASCII value + 1", while the codeword 4 encodes two digits using "130 + numeric value."

It has four codewords to encode, therefore we choose the minimum size of the symbol to encode: it is the symbol of size 12x12, offering a data matrix of size 10x10 and 12 codewords to encode compounds 5 codewords and data correction codewords 7. Knowing that 5 codewords data are needed and that we do not have that 4, a codeword filling will be added: it is the codeword value "129", which is always the first to indicate the end of data. It is not necessary to calculate other using the 253-state algorithm.

Codeword	ASCII value	Binary value
C5	129	1000 0001

Compared to what we saw earlier, we know that:

n = 12, the total number of codewords
k = 5, the number of data codewords
2t = 7, the number of correction codewords
the polynomiali(x) = 70 x⁴ + 79 x³ + 68 x² + 131 x + 129
the polynomial i(x) x^n-k = 70 x¹¹ + 79 x¹⁰ + 68 x⁹ + 131 x⁸ + 129 x⁷.

As a reminder, the operations occur in GF(2⁸). With the algorithms presented above, the generator polynomial was calculated:

g(x) = x⁷ + 254 x⁶ + 92 x⁵ + 240 x⁴ + 134 x³ + 144 x² + 68 x + 23

The calculation of the codewords representing polynomial correction is performed like this:

(i(x) x^n-k) = 4 x⁶ + 133 x⁵ + 98 x⁴ + 49 x³ + 253 x² + 53 x + 182

The correction codewords, corresponding to the coefficients of the polynomial are:

Codeword	ASCII value	Binary value
C6	4	0000 0100
C7	133	1000 0101
C8	98	0110 0010
C9	49	0011 0001
C10	253	1111 1101
C11	53	0011 0101
C12	182	1011 0110

Must then place these codewords in the data matrix according to the appropriate algorithm. The order of placement is as follows:

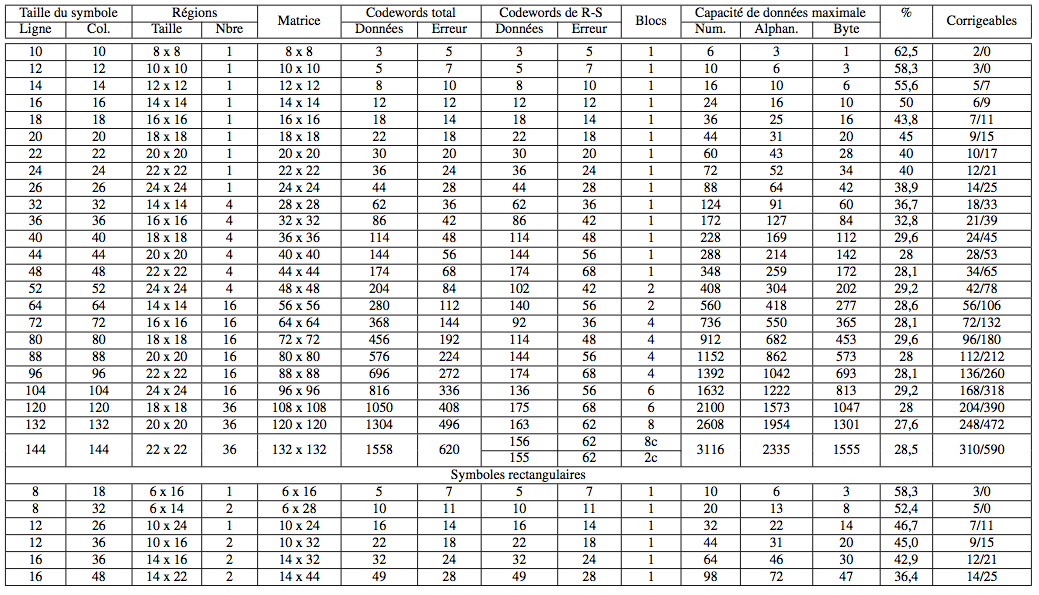
Summary table of data Data Matrix

Barcode Generator Data Matrix Online

Please enter the code: