CODE BARRES DATA MATRIX
Format du DATA MATRIX
| Longueur | Type | Système de correction d'erreur |
|---|---|---|
| de 1 à 3116 caractères (variable) | numérique, alphanumérique ou byte |
oui (Reed-Solomon) |
La taille du symbole, représentation graphique, est déterminée selon la nature et le nombre de données à encoder.
Une structure intermédiaire de 8 bits est utilisée pour enregistrer chaque donnée : le codeword.
Le symbole est composé de 3 groupes de codewords, placés les uns après les autres :
- Les codewords de données : calculés à partir des données
- Les codewords remplissage : facultatifs, remplissent le symbole lorsque les codewords de données ne suffisent pas
- Les codewords de correction : calculés à partir des codewords de données et de remplissage à l'aide de l'algorithme de Reed-Solomon, qui permettent de retrouver une partie des données lors d'un effacement ou d'une mauvaise lecture du décodeur.
L'encodage se déroule en deux étapes :
- Encodage de haut niveau : consiste à transformer les données en une série de codewords et à calculer les codewords de remplissage et de correction correspondants
- Encodage de bas niveau : consiste à placer ces codewords dans la matrice de données.
Représentation graphique du code barres Data Matrix
Le symbole est composé de petits carrés noirs et blancs juxtaposés, appelés modules.
Un module représente un bit : généralement en noir pour le 1 et en blanc pour le 0.
Le Data Matrix peut être de forme carrée (la plus utilisée) ou rectangulaire.
On peut décomposer le symbole en trois parties :
- Les motifs de repérage, ou « finder pattern », qui forment le contour des données. On retrouve deux segments adjacents représentant un L, composés de modules noirs uniquement afin de déterminer le sens et l'orientation des données. Les deux côtés opposés alternent les modules noirs et blancs afin de déterminer la taille d'un module et donc du symbole, mais également afin de délimiter le symbole
- La zone de silence, ou « quiet zone », qui est une zone blanche d'au moins un module située autour des motifs de repérage, afin que le décodeur ne soit pas gêné lors de la lecture
- La matrice de données qui est composée de modules sous forme d'une matrice et qui se situe au centre des motifs de repérage.
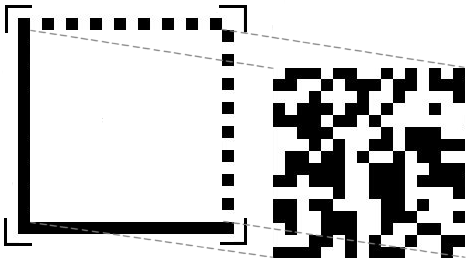
Lorsque le symbole dépasse une certaine limite de taille, le symbole est divisé en plusieurs zones de données, les régions, qui sont délimités par des motifs de repérage internes. Quatre types de division en régions existent : 3 pour la forme carrée et 1 pour la forme rectangulaire.

Encodage de haut niveau
Six modes d'encodage coexistent : ASCII, Text, C40, X12, EDIFACT et Base 256. L'encodage ASCII est l'encodage par défaut et le plus utilisé. Il sera le seul présenté ici.
L'ensemble des valeurs des codewords du mode ASCII sont visibles dans le tableau suivant :
| Valeur du Codeword | Correspondance |
|---|---|
| 1 - 128 | Caractères ASCII (valeur ASCII + 1) |
| 129 | Premier caractère de remplissage |
| 130 - 229 | Nombres entre 00 et 99 (valeur numérique + 130) |
| 230 | Caractère d'enclenchement du mode C40 |
| 231 | Caractère d'enclenchement du mode base 256 |
| 232 | Caractère FNC1 |
| 233 | Caractère "Structured Append" |
| 234 | Caractère "Reader Programming" |
| 235 | Upper Shift (passage à l'ASCII étendu) |
| 236 - 237 | 05 Macro - 06 Macro |
| 238 | Caractère d'enclenchement du mode X12 |
| 239 | Caractère d'enclenchement du mode Text |
| 240 | Caractère d'enclenchement du mode EDIFACT |
| 241 | Caractère ECI |
| 242 - 255 | Pas utilisés dans le mode ASCII |
Certaines valeurs ne sont pas explicitées car non utilisées.
Dans le mode ASCII, les données sont encodées selon 3 possibilités :
- La valeur du codeword d'un caractère ASCII non étendu (valeur dans l'interval 0 à 127) vaut « valeur ASCII + 1 »
- Pour un caractère ASCII étendu (valeur dans l'interval 128 à 255), deux codewords sont utilisés : le premier, appelé Upper Shift, vaut « 235 » et le second vaut « valeur ASCII - 127 »
- On peut également enregistrer deux chiffres successifs (ex : 27) en un seul codeword qui vaut « valeur numérique + 130 ».
Lorsque le nombre de codewords de données ne peut remplir complètement la partie « données » de la plus petite taille de symbole possible, des codewords de remplissage sont ajoutés. Le premier de ces codewords, qui indique la fin des données dans ce cas, vaut toujours « 129 ». La suite est calculée grâce à l'algorithme 253-state suivant :
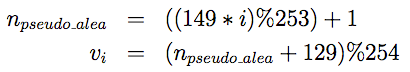
- avec "%" l'opération modulo et vi le codeword de remplissage à la position i
Calcul des codewords de correction
Les codes de Reed-Solomon sont utilisés comme système de correction d'erreurs. Ceux-ci ont une capacité de détection et de correction d'erreurs définie à l'avance, dépendant de la taille de la matrice de données.
Un corps C est un ensemble d'éléments fermé et muni de deux opérations binaires appelées addition et multiplication. Le fait d'être fermé implique que le résultat de chaque opération sur deux éléments de l'ensemble donnera toujours un élément de l'ensemble.
Il existe de nombreux corps, finis et infinis. Il s'avère que pour tout entier premier p et pour tout entier n (>=1), il existe un corps fini unique avec np éléments, que l'on note GF(np). Ces corps sont appelés Corps de Galois.
On peut représenter les éléments de GF(np) à l'aide des éléments de base a : 0, 1, a, a2, a3, ..., a(n-1). Prenons un exemple :
- a3 + a + 1
Les éléments peuvent également être représentés sous différentes formes : en binaire, en décimal ou même sous la forme d'un polynôme. Pour le même exemple, sous la forme :
- binaire : 1011 (0 correspond à l'absence de a2)
- décimale : 11 (8+2+1)
- polynômiale : a3 x3 + a x + 1
Pour chaque corps de Galois, il existe au moins un polynôme primitif, noté p(x), qui permet de construire le corps. Les Data Matrix stockant les données sur 8 bits (dans des codewords), ils travaillent donc dans le corps de Galois GF(28). Ils utilisent le polynôme primitif x8+x5+x3+x2+1, qui correspond à la valeur 301.
L'addition et la soustraction de deux éléments consiste en la fonction XOR (OU exclusif) entre ces deux éléments. La multiplication et la division sont calculés en multipliant les polynômes correspondant. Cette opération étant relativement coûteuse en temps de calcul, un algorithme est utilisé. Sachant que tous les éléments sont une puissance du polynôme primitif p, il faut donc chercher pour chaque élément c la puissance i telle que :
- i = logp (c)
- c = antilogp (i)
A partir de là, on peut calculer pour deux éléments c et d :
- c * d = antilogp (logp(c) + logp(d))
- c / d = antilogp (logp(c) - logp(d))
On peut obtenir le tableau des antilogs e grâce à cet algorithme :
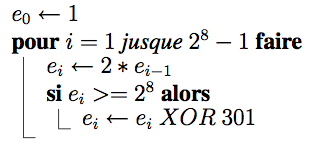
Un code de Reed-Solomon de taille n avec k données est noté RS(n,k). Il y a donc n-k = 2t symboles de contrôle et ce code permet de corriger jusqu'à t symboles erronés. Le nombre de symboles de contrôle est défini par la taille du Data Matrix.
L'équation clé pour le codage d'un code RS(n,k) est :
- c(x) = i(x) xn-k + [i(x) xn-k] modulo g(x)
avec
- c(x) : le polynôme final
- i(x) : le polynôme de données
- [i(x) xn-k] modulo g(x) : le polynôme de contrôle
- g(x) : le polynôme générateur
Les 2t symboles de contrôle sont calculés à partir d'un polynôme générateur de puissance 2t, composé de 2t + 1 termes, qui est de la forme suivante :
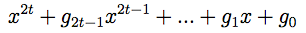
Il y a 16 longueurs de bloc de Reed-Solomon possible (voir tableau récapitulatif). Les coefficients des polynômes générateurs peuvent être calculés grâce à l'algorithme suivant :

Le polynôme générateur étant calculé, il suffit de suivre l'équation afin d'obtenir le polynôme de contrôle : il s'agit du reste de la division entre le polynôme de données et le polynôme générateur. Les coefficients correspondent aux codewords de contrôle.
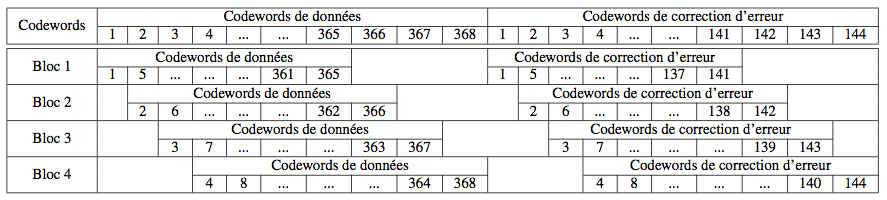
Pour les symboles Data Matrix contenant un total de moins de 255 codewords (tous les symboles rectangulaires et les carrés de tailles inférieures à 48x48), les codewords de correction sont calculés directement à partir des codewords de données. Pour les autres symboles, les codewords de correction sont calculés en suivant une procédure d'entrelacement : on divise les codewords de données en plusieurs blocs de tailles identiques et les codewords de correction sont calculés bloc par bloc. Chaque codeword c fait parti du groupe :
- c modulo n
avec n le nombre de blocs pour le symbole
Pour simplifier, pour n blocs, le premier groupe est formé des codewords de données 1, n+1, 2n+1, 3n+1, ... le second est formé des codewords de données 2, n+2, 2n+2, 3n+2, ...
Un exemple d'entrelacement peut être visualisé ci-après :
Encodage de bas niveau
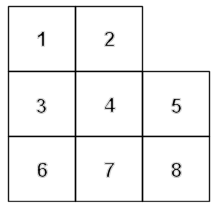
Chaque codeword est représenté dans la matrice de données par un carré partiel de 8 modules, correspondant à 8 bits. Le module 1 possède la valeur du bit le plus signifiant (valeur 128) alors que le module 8 possède la valeur du bit le plus insignifiant (valeur 1).
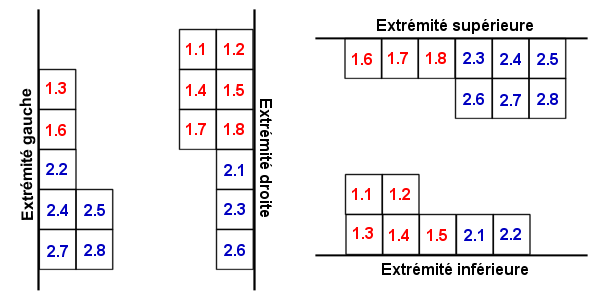
Il se peut cependant qu'un codeword ne peut être contenu entièrement dans la matrice à un certain emplacement. Ceux-ci peuvent alors être séparés en plusieurs parties (2 ou 3) afin d'être continué de l'autre côté du symbole.
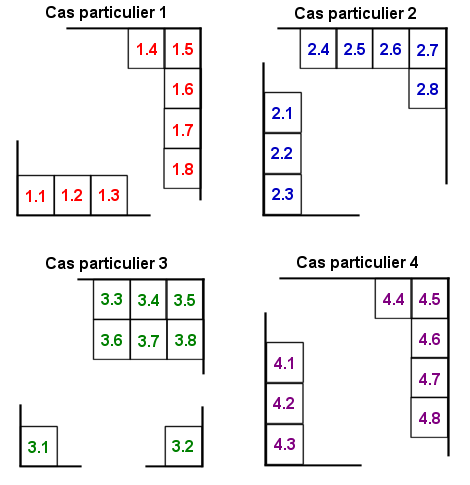
De plus, dans quatre cas particuliers, les codewords placés dans les coins peuvent être également placé de façon différente.
Le placement dans la matrice suit un certain ordre. Les premiers codewords sont toujours placés comme ceci :
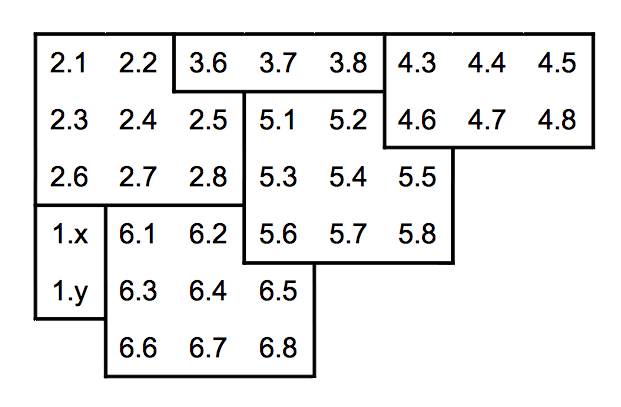
Les codewords sont ensuite emboîtés les uns dans les autres, en suivant des lignes obliques (45°) parallèles. Le sens des obliques est identique une fois sur deux.
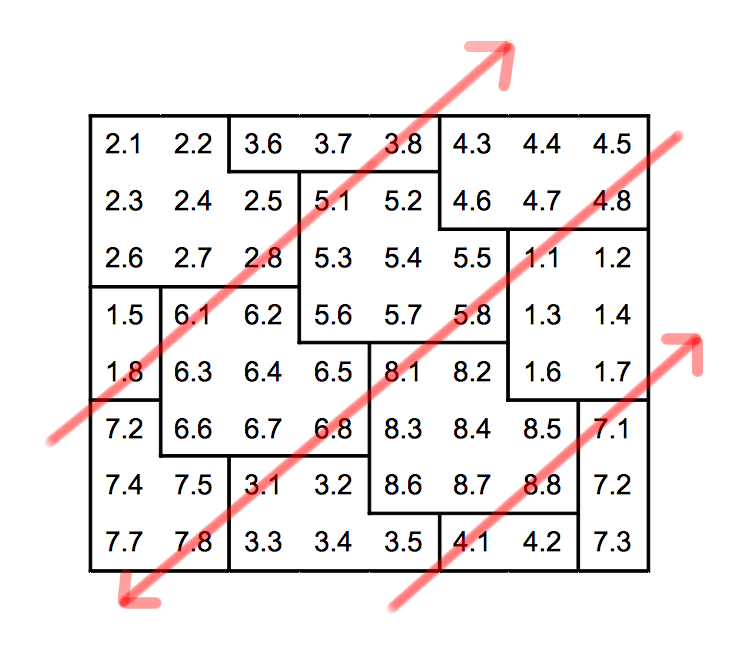
Il se peut, selon la taille du symbole, que les quatres modules du coin inférieur droit soient vides. Les symboles 12x12 par exemple, dont la matrice de données est de 10x10, donnent 100 modules dans lesquels 12 codewords peuvent être insérés. Sachant qu'un codeword rempli 8 modules, un total de 96 modules seront occupés et les 4 derniers seront donc vides. Pour les remplir, on utilise des modules noirs et blancs alternés comme présenté ci-dessous :
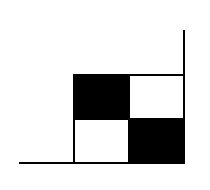
Il faudra ensuite ajouter le finder pattern principal et éventuellement les finder pattern internes si le nombre de régions est supérieur à 1.
Exemple d'encodage
Supposons que l'on veuille encoder « ENC01 ». Les valeurs ascii des différents caractères sont :
| E | N | C | 0 | 1 |
| 69 | 78 | 67 | 48 | 49 |
Selon le mode ASCII, les valeurs des codewords seront :
| Codeword | Méthode | Evaluation | Valeur mode ASCII | Equivalent binaire |
|---|---|---|---|---|
| C1 | Valeur ASCII + 1 | 69 + 1 | 70 | 0100 0110 |
| C2 | Valeur ASCII + 1 | 78 + 1 | 79 | 0100 1111 |
| C3 | Valeur ASCII + 1 | 67 + 1 | 68 | 0100 0100 |
| C4 | Valeur numérique + 130 | 1 + 130 | 131 | 1000 0011 |
La valeur des codewords 1, 2 et 3 ont été calculés simplement en utilisant la « valeur ASCII + 1 », alors que le codeword 4 encode deux chiffres successifs en utilisant « valeur numérique + 130 ».
On a donc 4 codewords à encoder, on choisit dès lors, la taille minimale de symbole permettant de les encoder : il s'agit du symbole de taille 12x12, proposant une matrice de données de taille 10x10 et permettant d'encoder 12 codewords composés de 5 codewords de données et de 7 codewords de correction. Sachant que 5 codewords de données sont nécessaires et que nous n'en possédons que 4, un codeword de remplissage va être ajouté : il s'agit du codeword de valeur « 129 », qui est toujours le premier afin d'indiquer la fin des données. Il n'est pas nécessaire d'en calculer d'autres à l'aide de l'algorithme 253-state.
| Codeword | Valeur mode ASCII | Equivalent binaire |
|---|---|---|
| C5 | 129 | 1000 0001 |
Par rapport à ce qu'on a vu précédemment, on sait que :
- n = 12, le nombre de codewords total
- k = 5, le nombre de codewords de données
- 2t = 7, le nombre de codewords de correction
- le polynôme i(x) = 70 x4 + 79 x3 + 68 x2 + 131 x + 129
- le polynôme i(x) xn-k = 70 x11 + 79 x10 + 68 x9 + 131 x8 + 129 x7.
Pour rappel, les opérations se passent dans GF(28). Grâce aux algorithmes présentés précédemment, le polynôme générateur a été calculé :
- g(x) = x7 + 254 x6 + 92 x5 + 240 x4 + 134 x3 + 144 x2 + 68 x + 23
Le calcul du polynôme représentant les codewords de correction est effectué comme ceci :
- (i(x) xn-k) = 4 x6 + 133 x5 + 98 x4 + 49 x3 + 253 x2 + 53 x + 182
Les codewords de correction, correspondant aux coefficients de ce polynôme sont les suivants :
| Codeword | Valeur mode ASCII | Equivalent binaire |
|---|---|---|
| C6 | 4 | 0000 0100 |
| C7 | 133 | 1000 0101 |
| C8 | 98 | 0110 0010 |
| C9 | 49 | 0011 0001 |
| C10 | 253 | 1111 1101 |
| C11 | 53 | 0011 0101 |
| C12 | 182 | 1011 0110 |
Il faut ensuite placer ces différents codewords dans la matrice de données en suivant l'algorithme adéquat. L'ordre de placement est le suivant :

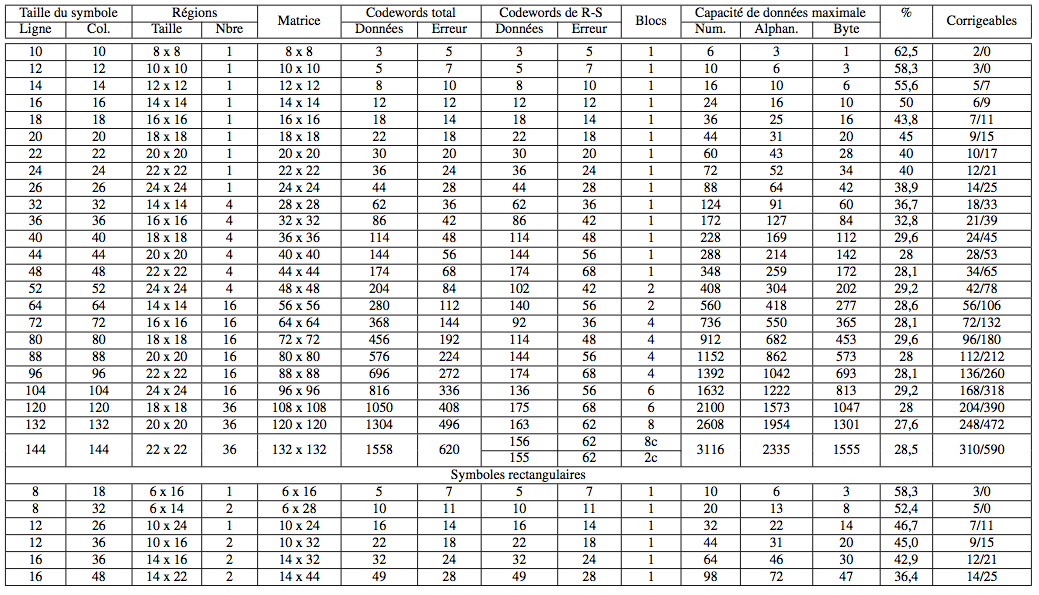
Tableau récapitulatif des données des Data Matrix
Générateur de code barres Data Matrix en ligne
Veuillez saisir le code :